Basic Sorting Algorithms
목차
Selection sort(선택 정렬)
Insertion sort(삽입 정렬)
Heap sort(힙 정렬)
Quick sort(퀵 정렬)
merge sort(병합 정렬)
- Bubble sort (거품 정렬)
· 시간 복잡도: 평균과 최악의 경우 O(N^2), 최선의 경우 O(N)
· 방법은 오른쪽으로 i와 i + 1번 째를 비교하면서 뒤로 제일 큰 것을 이동시키는 것이다.
· 최선의 경우는 스와핑이 한번도 일어나지 않는 경우이다.
· 이름의 유래는 아래 이미지를 90도 회전시켜서 볼 경우 위로 올라가는 것이 거품과 같다하여 붙여진 이름이다.
public class BubbleSort {
static int[] data = {14, 6, 45, 43, 41, 28, 38, 36, 49, 16, 34};
public static void main(String[] args) {
bubbleSort();
for (int i = 0; i < data.length; i++) {
System.out.print(data[i]);
if (i < data.length - 1) System.out.print(" ");
}
}
public static void bubbleSort() {
boolean isSwapped;
for (int i = 0; i < data.length; i++) {
isSwapped = false;
for (int j = 1; j < data.length - i; j++) {
if (data[j] < data[j - 1]) {
int tmp = data[j - 1];
data[j - 1] = data[j];
data[j] = tmp;
isSwapped = true;
}
}
if (!isSwapped) break;
}
}
}
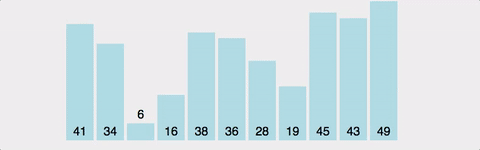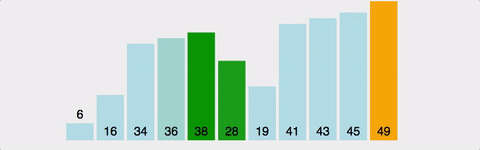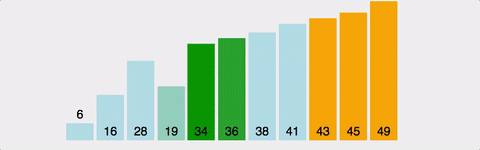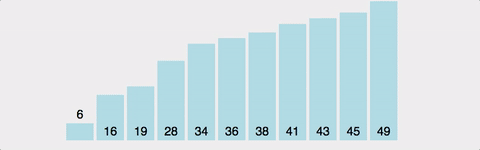
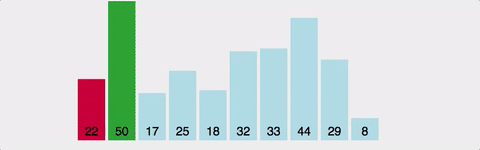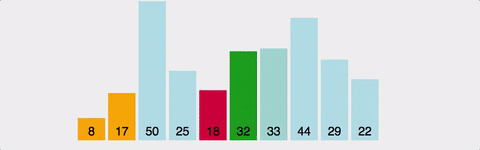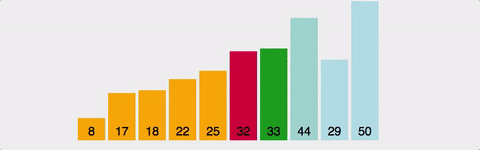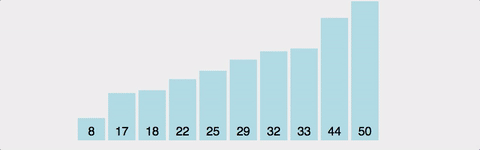
- selection sort(선택 정렬)
· 시간 복잡도: 평균과 최악과 최선 모든 경우 O(N^2)
· 방법은 i와 j(i + 1 ~ array.length - 1)를 비교하여 위치를 변경하여 작은 값을 왼쪽으로 보내는 것이다.
· 이 경우, 최선의 경우도 O(N)인데, 그 이유는 i와 비교하는 대상이 j이기 때문에, 다음 i와의 상관 관계가 없기 때문이다.
public class SelectionSort {
static int[] data = {14, 6, 45, 43, 41, 28, 38, 36, 49, 16, 34};
public static void main(String[] args) {
selectionSort();
for (int i = 0; i < data.length; i++) {
System.out.print(data[i]);
if (i < data.length - 1) System.out.print(" ");
}
}
public static void selectionSort() {
for (int i = 0; i < data.length - 1; i++) {
for (int j = i + 1; j < data.length; j++) {
if (data[i] > data[j]) {
int tmp = data[i];
data[i] = data[j];
data[j] = tmp;
}
}
}
}
}
- Insertion sort(삽입 정렬)
· 시간 복잡도: 평균과 최악의 경우 O(N^2), 최선의 경우 O(N)
· 방법은 0번 째 인덱스가 아니라 1번 째 인덱스부터 시작하여 이전 값들을 확인하여, 자신의 적절한 위치를 확인하여 삽입한다.
· 최선의 경우는 입력이 정렬되어있는 경우이다. 이 이유는 이전 값들을 확인할 때 자신의 위치를 바로 찾고 탈출하기 때문이다.
public class InsertionSort {
static int[] data = {14, 6, 45, 43, 41, 28, 38, 36, 49, 16, 34};
public static void main(String[] args) {
insertionSort();
for (int i = 0; i < data.length; i++) {
System.out.print(data[i]);
if (i < data.length - 1) System.out.print(" ");
}
}
public static void insertionSort() {
for (int i = 1; i < data.length; i++) {
int tmp = data[i], here = i - 1;
for (int j = i - 1; j > -1; j--) {
if (data[j] > tmp) data[j + 1] = data[j];
else {
here = j + 1;
break;
}
}
data[here] = tmp;
}
}
}
- Heap sort(힙 정렬)
· 시간 복잡도: 평균과 최악과 최선 모든 경우 O(NlogN)
· Heap의 원리로 작동한다.
·
import java.util.PriorityQueue;
import java.util.Queue;
public class HeapSort {
static int[] data = {6, 5, 3, 1, 8, 7, 2, 4};
static Queue priorityQueue = new PriorityQueue();
public static void main(String[] args) {
for (int i = 0; i < data.length; i++) {
priorityQueue.add(data[i]);
}
heapSort();
}
public static void heapSort() {
while (!priorityQueue.isEmpty()) System.out.print(priorityQueue.poll() + " ");
}
}
- Quick sort(퀵 정렬)
· 시간 복잡도: 평균과 최선의 경우 O(NlogN), 최악의 경우 O(N^2)
· 퀵 정렬은 Java에서도 library에 구현될 정도로 일반적으로 많이 사용하는 정렬 방법이다.
· Java의 Arrays.sort()에서는 배열의 크기가 작을 때는 내부적으로 insertion sort를 사용하고, 비교할 것이 많아지면 quick sort를 사용도록 구현되어 있다고 한다.
· 방법은 D&C 즉, 분할정복을 이용한 방법이다.
· 최악의 경우는 입력으로 주어진 배열이 정렬이 되어있고, pivot을 첫 번째 인덱스로 선택할 때 발생한다. 그 이유는 left는 pivot보다 무조건 크기 때문에 1번째 인덱스에 멈춰있고, right가 n번의 비교를 통해 0이되면 한 라운드가 종료된다. 마치 selection sort처럼 진행하게 된다.
1.pivot을 정한다. (여기서는 중간 값)
2.왼쪽에서부터 값이 pivot보다 큰 index(left 변수)를 찾는다, 동시에 오른쪽에서부터 값이 pivot보다 작은 index(right 변수)를 찾는다.
3.case1 - (left <= right)
Swapping을 하고, (left > right)일 때까지 2.을 반복한다.
3.case2 - (left > right)
반복문을 탈출하여 분기한다.
✔︎ 왜 같을 때도 Swapping을 하는가? (left == right)인 상황에서 탈출하여 분기하면 l ~ right, left ~ r, 로 각각 분기하는데
겹치는 영역(right, left)이 발생하여 첫 번째 분기점에서 실행되어 arr[right]인 지점의 값이 변경되고, 이후 두 번째 분기에서 arr[left]의 값이 변경되면 sorting 의 결과가 이상해지고, 무한 calling이 발생한다.
if (left < right) swap 인 경우
예제) arr = [14, 6, 45, 43, 41]
pivot = 45, left = 0, right = 4;
do while안의 while을 각각 실행 후,
left = 4, right = 4
스왑 안하고 탈출한다면, l ~ right인 분기를 또 타게 된다.
public class QuickSort {
static int[] data = {14, 6, 45, 43, 41, 28, 38, 36, 49, 16, 34};
public static void main(String[] args) {
quickSort(data, 0, data.length - 1);
for (int i = 0; i < data.length; i++) {
System.out.print(data[i]);
if (i < data.length - 1) System.out.print(" ");
}
}
public static void quickSort(int[] arr, int l, int r) {
int left = l, right = r;
int pivot = arr[(l + r) / 2];
do{
while (arr[left] < pivot) left++; // find index that higher than pivot
while (arr[right] > pivot) right--;// find index that lower than pivot
if (left <= right) {
int tmp = arr[left];
arr[left] = arr[right];
arr[right] = tmp;
left++;right--;
}
}while (left < right);
if (l < right) quickSort(arr, l, right);
if (r > left) quickSort(arr, left, r);
}
}
- merge sort(병합 정렬)
· 시간 복잡도: 평균과 최악과 최선 모든 경우 O(N^2)
· 방법은 D&C의 아이디어를 사용하여 배열을 나눴다가 합치는 방식으로 진행한다.
· 장점은 제한된 메모리 환경에서 병합정렬을 사용할 수 있다는 점이다.
· 단점은 제자리에서 교체하는 방법 in-place sorting이 아닌 배열만큼의 공간을 더 사용하기 때문에 공간 복잡도가 다른 정렬에 비해 높다.
public class MergeSort {
static int[] sortedArray = new int[11];
public static void main(String[] args) {
int[] data = {14, 6, 45, 43, 41, 28, 38, 36, 49, 16, 34};
mergeSort(data, 0, data.length - 1);
for (int i = 0; i < sortedArray.length; i++) {
System.out.print(sortedArray[i]);
if (i < sortedArray.length - 1) System.out.print(" ");
}
}
public static void mergeSort(int[] arr, int m, int n) {
int mid;
if (m < n) {
mid = (m + n) >> 1;
mergeSort(arr, m, mid);
mergeSort(arr, mid + 1, n);
merge(arr, m, mid, n);
}
}
public static void merge(int[] arr, int m, int mid, int n) {
int i = m, j = mid + 1, k = m;
while (i <= mid && j <= n) {
sortedArray[k] = (arr[i] <= arr[j]) ? arr[i++] : arr[j++];
k++;
}
int start = (i > mid) ? j : i, end = (i > mid) ? n : mid;
for (int t = start; t <= end; t++, k++) {
sortedArray[k] = arr[t];
}
for (int t = m; t <= n; t++) {
arr[t] = sortedArray[t];
}
}
}
일반적으로 퀵소트와 머지소트가 비교되는데 배열을 사용하는 경우라면 퀵소트를 리스트를 사용하는 경우라면 머지소트를 사용하는 것이 좋다.
그 이유는 퀵소트는 인덱스를 이용하여 정렬을 하고, 머지소트는 리스트를 쪼개서 정렬을 하기 때문이다.
마지막으로 stable & unstable sort에 대해서 정리를 해보자.
stable: 같은 값을 가진 i, j가 sort 전 후 위치가 서로 바뀌지 않는 경우.
unstable: 같은 값을 가진 i, j가 sort 전 후 위치가 서로 바뀌는 경우.
stable: bubble, insertion, merge
unstable: selection, heap, quick
이미지 출처: https://cdn-images-1.medium.com